Programming a Guitar Tuner with Python
Contents
1. Introduction
Hello there! In this post we will program a guitar tuner with Python. This project is a pure software project, so there is no soldering or tinkering involved. You just need a computer with a microphone (or an audio interface) and Python. Of course the algorithms presented in the post are not bound to Python, so feel free to use any other language if you don't mind the addtional translation (however, I recommend to not use tcl as it is "the best-kept secret in the software industry" and we better keep it a secret, lol).
We will start with analyzing the problem we have which is probably a detuned guitar and then forward to solving this problem using math and algorithms. The focus of this post lies on understanding the methods we use and what their pros and cons are. For those who want to code a guitar tuner in under 60 seconds: my Github repo ;)
2. Guitars & Pitches
Let's start with some really basic introduction to music theory and guitars. First, we have to define some important musical terms as an exact distinction will avoid some ambiguities:
- The frequency is defined as the reciprocal of the period duration of an repeating event. For example, if we have a sinusoidal signal with a period length of 2ms, the frequency is 500Hz.
- Pitch is the perceived frequency of a sound. Thus, in contrast to frequency which is physical measure, the pitch is a psychoacoustical measure. This distinction is needed as there are cases where we hear frequencies which are physically not there (or don't hear frequencies which are actually there)! Don't worry, we will have a closer look on that subject later.
- A note is just a pitch with a name. For example, the well known A4 is a pitch at 440Hz. It can also carry temporal information like whole notes or half notes, but this is rather uninteresting for us.
- The term tone seems to be ambigous, so we rather try to avoid it. The only kind of tone which will be used is a pure tone. A pure tone is a sound with a sinusoidal waveform.
With this defintions in mind we will now look at how a guitar works on a musical level. I guess most of you know this but the "default" guitar has 6 strings which are usually tuned in the standard tuning EADGBE. Whereby each note refers to one of the strings. For example, the lowest string is tuned to the note E2. This means that the string has a pitch of 82.41Hz, since this is how the tone E2 is defined. If it would have a pitch of 81Hz, our guitar is out-of-tune and we have to use the tuners on the headstock to get it back in tune. Of course all other notes can be assigned to a certain pitch as well:
Note, that for this post we assume an equal temperament
and a concert pitch of A4=440Hz which covers probably 99% of modern music.
The cool thing about the equal temperament is that it defines the notes and pitches in half step fashion described by the following formula:
$$f(i) = f_0 \cdot 2^{i/12} $$
So, if you have a pitch \(f_0\), for example A4 at 440Hz, and you want to increase it by one half step to an A#4 then you have to multiply
the pitch 440Hz with \(2^{1/12}\) resulting in 466.16Hz.
We can also derive an inverse formula which tells how many half steps are between the examined pitch \(f_i\) and a reference pitch \(f_o\).
$$12 \cdot log_2 \left( \frac{f_i}{f_o} \right) = i $$
This also allows us to assign a pitch a note. Or at least a note which is close to the pitch.
As you can imagine, this formula will be of particular interest for us.
Because if we can extract the pich from a guitar recoding, we want to know the closest note and how far away it is.
This leads us to the following Python function
CONCERT_PITCH = 440
ALL_NOTES = ["A","A#","B","C","C#","D","D#","E","F","F#","G","G#"]
def find_closest_note(pitch):
i = int(np.round(np.log2(pitch/CONCERT_PITCH)*12))
closest_note = ALL_NOTES[i%12] + str(4 + (i + 9) // 12)
closest_pitch = CONCERT_PITCH*2**(i/12)
return closest_note, closest_pitchAs next step we need to record the guitar and determine the pitch of the audio signal. This is easier said than done as you will see ;)
3. Pitch Detection
After reading the following section you hopefully know what is meant by pitch detection and which algorithms are suited for this. As already mentioned above, pitch and frequencies are not the same. This might sound abstract at first, so let's "look" at an example.
The example is a short recording of me playing the note A4 with a pitch of 440Hz on a guitar.import sounddevice as sd
import scipy.io.wavfile
import time
SAMPLE_FREQ = 44100 # Sampling frequency of the recording
SAMPLE_DUR = 2 # Duration of the recoding
print("Grab your guitar!")
time.sleep(1) # Gives you a second to grab your guitar ;)
myRecording = sd.rec(SAMPLE_DUR * SAMPLE_FREQ, samplerate=SAMPLE_FREQ, channels=1,dtype='float64')
print("Recording audio")
sd.wait()
sd.play(myRecording, SAMPLE_FREQ)
print("Playing audio")
sd.wait()
scipy.io.wavfile.write('example1.wav', SAMPLE_FREQ, myRecording)
The same example but now visualized as a time/value graph looks like follows
import scipy.io.wavfile
import matplotlib.pyplot as plt
import numpy as np
sampleFreq, myRecording = scipy.io.wavfile.read("example1.wav")
sampleDur = len(myRecording)/sampleFreq
timeX = np.arange(0,sampleDur, 1/sampleFreq)
plt.plot(timeX, myRecording)
plt.ylabel('x(k)')
plt.xlabel('time[s]')
plt.show()
As you can see the signal has a period length of roughly 2.27ms which corresponds to a frequency of 440Hz. So far so good. But you can also see that the signal is far away from being a pure tone. So, what is happening there?
To answer this question we need to make use of the so-called Discrete Fourier Transform (DFT).
It's basically the allround tool of any digital signal processing engineer.
From a mathematical point of view it shows how a discrete signal can be decomposed as a set of cosine functions
oscillating at different frequecies.
Or in musical terms: the DFT shows which pure tones can be found in an audio recording.
If you are interested in the mathematical details of the DFT, I recommend you to read my previous
post.
But no worries, the most important aspects will be repeated in this post.
The cool thing about the DFT is that it provides us with a so called magnitude spectrum. For the given example it looks like this:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import scipy.io.wavfile
import matplotlib.pyplot as plt
import numpy as np
from scipy.fftpack import fft
sampleFreq, myRecording = scipy.io.wavfile.read("example1.wav")
sampleDur = len(myRecording)/sampleFreq
timeX = np.arange(0, sampleFreq/2, sampleFreq/len(myRecording))
absFreqSpectrum = abs(fft(myRecording))
print(absFreqSpectrum)
plt.plot(timeX, absFreqSpectrum[:len(myRecording)//2])
plt.ylabel('|X(n)|')
plt.xlabel('frequency[Hz]')
plt.show()
On the x-axis you can see the frequencies of the pure tones while the y-Axis displays their intensity.
The spectrum reveals some interesting secrets which you couldn't see in the time domain. As expected there is a strong intensity of the pure tone at 440Hz. But there are other significant peaks at integer multiples of 440Hz. For example, 880Hz, 1320Hz, etc. If you are familiar with music you may know the name of these peaks: harmonics or overtones.
The reason for the overtones is quite simple. When you hit a guitar string you excite it to vibrate at certain frequencies.
Especially frequencies which form standing waves can vibrate for a long time.
These fulfill the boundary conditions that the string cannot move at the points where it is attached to the guitar (bridge and nut).
Thus, multiple overtones are also excited which are all multiples of the fundamental frequency. The following GIF visualizes this:
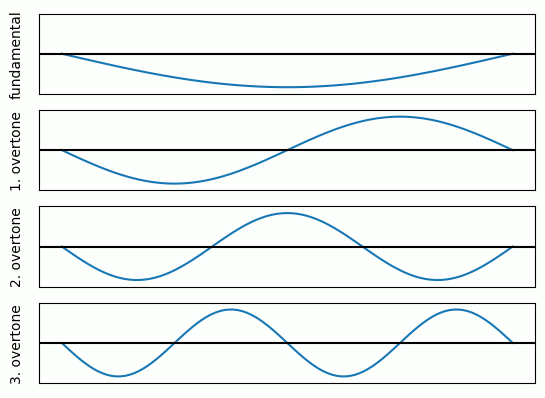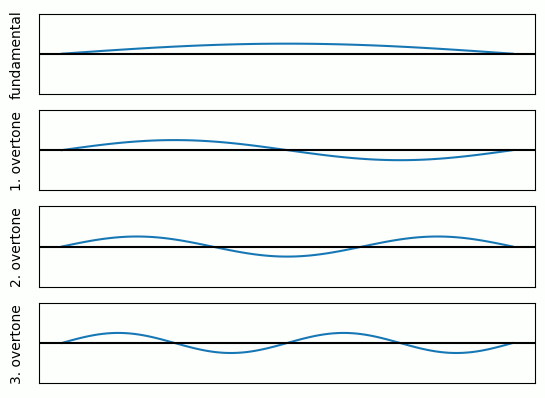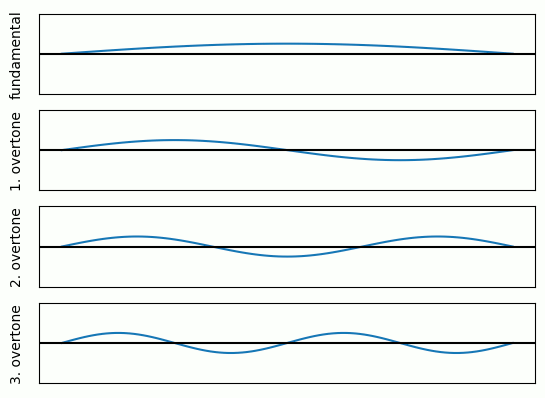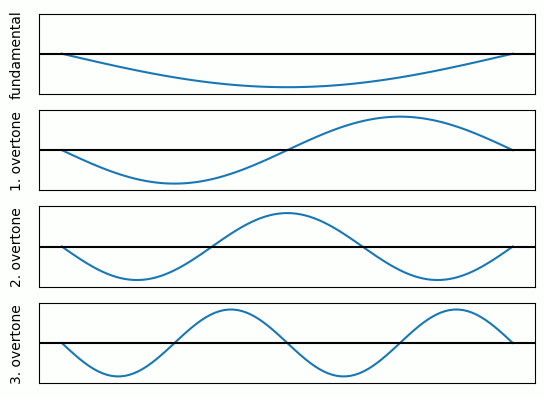
The overall set of harmonics and how they are related is called timbre.
A timbre is what makes your guitar sound like a guitar and not like any other instrument.
This is pretty cool on the one hand, but it makes pitch detection a real challenge.
Because at this point you might already had an idea for a guitar tuner: create a DFT spectrum, determine the frequency of the highest peak, done.
Well, for the given spectrum about this might work, but there are many cases for which you will get wrong results.
The first reason is that the fundamental frequency does not always have to create the highest peak.
Altough not beeing the highest peak the pitch is determined by it.
This is the reason why pitch detection is not just a simple frequency detection!
The second reason is that the power of the guitar signal is distributed over a large frequency band.
By selecting only the highest peak, the algorithm would be very prone to narrowband noise.
In the example spectrum given about you can see a high peak at 50Hz which is caused by mains hum.
Although the peak is relatively high, it does not determine the overall sound impression of the recording.
Or did you feel like the 50Hz noise was very present?
The complexity of this problem has lead to a number of different pitch detection algorithms. In order to choose the right algorithm we have to think about what requirements a guitar tuner needs to fullfill. The most important requirements surely are:
- Accuracy: According to [4], the human just-noticable difference for complex tones under 1000Hz is roughly 1Hz. So, our goal should roughly be a frequency resolution of 1Hz in a frequency range of ca. 80-400Hz.
- Realtime capabability: When using the tuner we want to have a live feedback about which note we play. We therefore have to consider things like the runtime complexity of the algorithm and the hardware we are using.
- Delay: If the results only popup 5 seconds after we played a string, tuning our guitar accurately will be pretty hard. I cannot provide you with any literature on that, but I guess a delay of lesser than 500ms sounds fair.
- Robustness: Even in noisy environments a guitar tuner should be capable of doing its job. Especially the omnipresent mains hum at 50Hz (or 60 Hz depending on where you live) shouldn't be a problem.
In the following we will start with programming a simple maximum frequency peak algorithm. As already mentioned above, this method may not work pretty well since the fundamental frequency is not guarenteed to always have the highest peak. However, this method is quite simple and a gentle introduction to this subject.
In the second the section a more sophisticated algorithm using the Harmonic Product Spectrums (HPS) is implemented. It is based on the simple tuner, so don't skip the first section ;)
3.1 Simple DFT tuner
Our first approach will be a simple guitar tuner using the DFT peak approach.
Usually the DFT algorithm is applied to the whole duration of signal.
However, our guitar tuner is a realtime application where there is no concept of a "whole signal".
Furthermore, as we are going to play several different notes, only the last few seconds are relevant for pitch detection.
So, instead we use the so called discrete Short-Time Fourier Transform (STFT) which is basically just the DFT applied for the most recent samples.
You can imagine it as some kind of window where new samples push out the oldest samples:
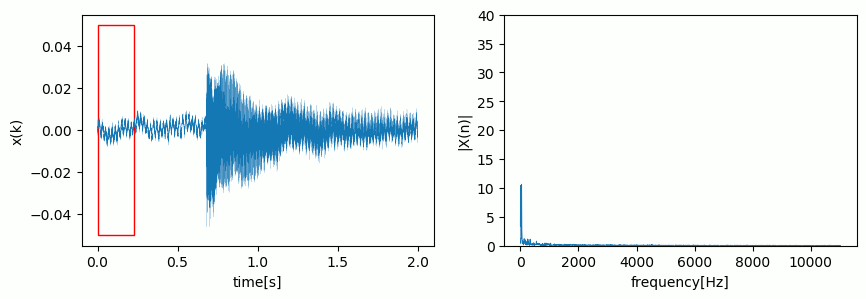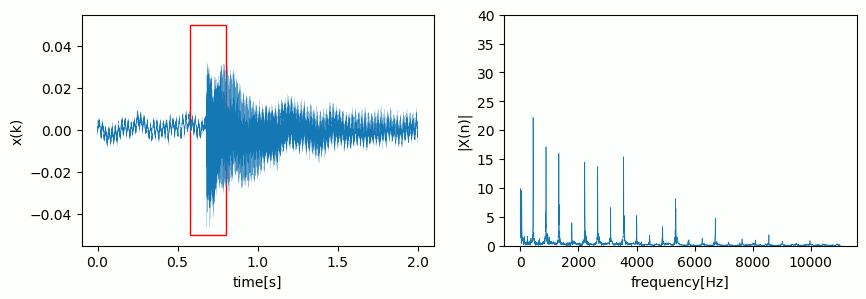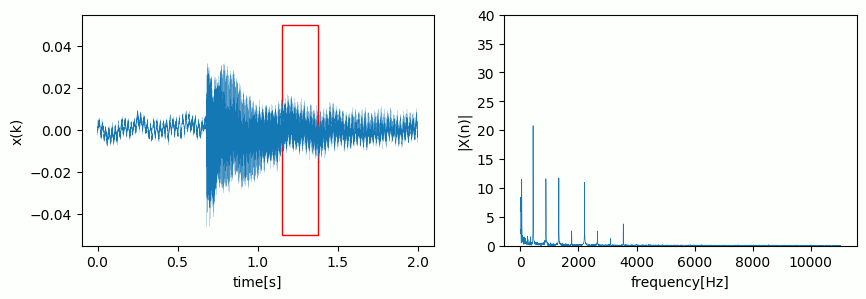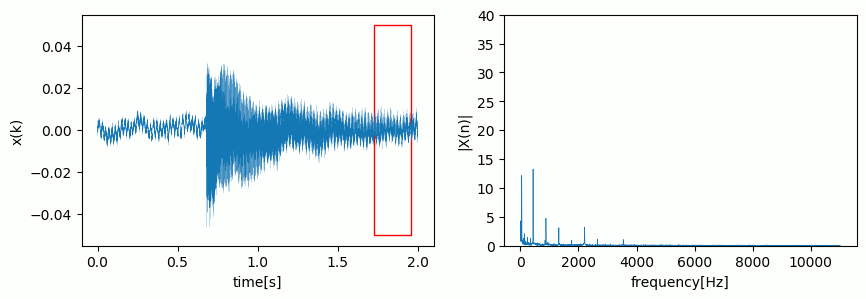Note, that the spectrum is now a so-called spectrogram as it varies over time.
Before we start with programming our tuner, we have to think about design considerations concerning the DFT algorithm. Because can the DFT fullfill the requirements we proposed above?
Let's begin with the frequency range.
The DFT allows you to analyze frequencies in the range of \( f < f_s / 2 \) with \(f_s\) beeing the sample frequency.
Typical sound recording devices use a sampling rate of around 40kHz giving us a frequency range of \(f < 20kHz\).
This is more than enough to even capture all the overtones.
Note, that the frequency range is an inherent property of the DFT algorithm, but there is also a close relation to the
Nyquist–Shannon sampling theorem.
The theorem states that you cannot extract all the information from a signal if the highest occuring frequencies
are greater than \(f_s / 2 \). This means the DFT is already working at the theoretical limit.
As a next point we look at the frequency resolution of the DFT which is (for details see my DFT post): $$ f_s / N \approx 1 / t_{window} [Hz]$$ With \(N\) being the window size in samples, and \(t_{window}\) the window size in seconds. The resolution in Hertz is approximately the reciprocal of the window size in seconds. So, if we have a window of 500ms, then our frequency resolution is 2Hz. This is where things become tricky as a larger window results in a better frequency resolution but negatively affects the delay. If we consider frequency resolution more important up to a certaint extent than delay, a windows size of 1s sounds like a good choice. With this setting we achieve a frequency resolution of 1Hz.
So far so good. If you convert all this knowledge to some code, your result might look like this:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
import sounddevice as sd
import numpy as np
import scipy.fftpack
import os
# General settings
SAMPLE_FREQ = 44100 # sample frequency in Hz
WINDOW_SIZE = 44100 # window size of the DFT in samples
WINDOW_STEP = 21050 # step size of window
WINDOW_T_LEN = WINDOW_SIZE / SAMPLE_FREQ # length of the window in seconds
SAMPLE_T_LENGTH = 1 / SAMPLE_FREQ # length between two samples in seconds
windowSamples = [0 for _ in range(WINDOW_SIZE)]
# This function finds the closest note for a given pitch
# Returns: note (e.g. A4, G#3, ..), pitch of the tone
CONCERT_PITCH = 440
ALL_NOTES = ["A","A#","B","C","C#","D","D#","E","F","F#","G","G#"]
def find_closest_note(pitch):
i = int(np.round(np.log2(pitch/CONCERT_PITCH)*12))
closest_note = ALL_NOTES[i%12] + str(4 + (i + 9) // 12)
closest_pitch = CONCERT_PITCH*2**(i/12)
return closest_note, closest_pitch
# The sounddecive callback function
# Provides us with new data once WINDOW_STEP samples have been fetched
def callback(indata, frames, time, status):
global windowSamples
if status:
print(status)
if any(indata):
windowSamples = np.concatenate((windowSamples,indata[:, 0])) # append new samples
windowSamples = windowSamples[len(indata[:, 0]):] # remove old samples
magnitudeSpec = abs( scipy.fftpack.fft(windowSamples)[:len(windowSamples)//2] )
for i in range(int(62/(SAMPLE_FREQ/WINDOW_SIZE))):
magnitudeSpec[i] = 0 #suppress mains hum
maxInd = np.argmax(magnitudeSpec)
maxFreq = maxInd * (SAMPLE_FREQ/WINDOW_SIZE)
closestNote, closestPitch = find_closest_note(maxFreq)
os.system('cls' if os.name=='nt' else 'clear')
print(f"Closest note: {closestNote} {maxFreq:.1f}/{closestPitch:.1f}")
else:
print('no input')
# Start the microphone input stream
try:
with sd.InputStream(channels=1, callback=callback,
blocksize=WINDOW_STEP,
samplerate=SAMPLE_FREQ):
while True:
pass
except Exception as e:
print(str(e))
This code should work out of the box, assuming that the corresponding python libraries are installed.
Here are some out-of-code comments which explain the single lines more in detail:
Line 1-4: Basic imports such as numpy for math stuff and sounddecive for capturing the microphone input
Line 7-12: Global variables
Line 14-22: The function for finding the nearest note for a given pitch. See section "Guitars & Pitches" for the detailed explaination.
Line 24-45: These lines are the heart of our simple guitar tuner, so a let's have a closer look.
Line 31-32: Here the incoming samples are appended to an array while the old samples are remmoved.
Thus, a window of WINDOW_SIZE samples is obtained.
Line 33: The magnitude spectrum is obtained by using the Fast Fourier Transform.
Note, that one half of the spectrum only provides redundant information.
Line 35-36: Here the mains hum is suppressed by simply setting all frequencies below 62Hz to 0.
This is still sufficient for a drop C tuning (C2=65.4Hz).
Line 38-40: First, the highest frequency peak is determined.
As a next step the highest frequencies is used to get the closest pitch and note.
Line 48-55: The input stream is initialized and runs in an infinite loop.
Once enough data is sampled, the callback function is called.
Line 42-43: Printing the results. Depending on your operating system a different clear function has to be called.
I also made a javascript version which works directly from you browser. Note, that it uses slightly different parameters. The corresponding magnitude spectrum is also visualized:
If you tried to tune your guitar using this tuner you probably noticed that it doesn't work pretty well. As expected there main problem are harmonic errors as the overtones are often more intense than the actual fundamental frequency. A way to deal with is problem is using the Harmonic Product Spectrums as the next section will show.
HPS tuner
In this section we will refine our simple tuner by using the so-called Harmonic Product Spectrum (HPS) which was introduced by A. M. Noll in 1969.
The idea behind it is quite simple yet clever.
The Harmonic Product Spectrum is a multiplication of \(R\) magnitude spectrums with different frequency scalings:
$$ Y(f) = \prod_{r=1}^{R} |X(fr)| $$
With \(X(f)\) being the magnitude spectrum of the signal.
I think that this is hard to explain in words, so let's take a look at a visualization for \(R=4\):
In the upper half of the visualization you can see the magnitude spectrums for the 440Hz guitar tone example.
Each with a different frequency scaling factor \(r\).
These magnitude spectrums are multiplied in a subsequent step resulting in the Harmonic Product Spectrum \(|Y(f)|\).
As the frequency scaling is always an integer number, the product vanishes for non-fundamental frequencies.
Thus, the last step is simply taking the highest peak of the HPS:
$$ f_{max} = \max_{f}{|Y(f)|} $$
For the given example the peak at 440Hz is perfectly determined.
In terms of frequency resolution and delay, the HPS tuner is pretty similar to the simple DFT tuner as the DFT is the basis of the HPS.
However, as the HPS uses the harmonies as well to determine the pitch a higher frequency resolution can be achieved if the spectrum is
interpolated and upsampled before the HPS process is executed.
Note, that upsampling and intepolating does not add any information to the spectrum but avoids information loss as the spectrum is effectively downsampled
when using different frequency scaling.
Let me illustrate this by using an intuitive example.
Assuming we have a DFT with a frequency resolution of 1Hz
and we have a peak at 1761 Hz from which we know that it is the 4th harmonic of a fundamental frequency at 440Hz in the spectrum.
If you have this information, you can calculate \(1761/4=440.25\) and conclude that the fundamental frequency is rather 440.25Hz than 440Hz.
The same principle is used by the HPS algorithm.
A python version of a HPS guitar tuner may look like this:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
'''
Guitar tuner script based on the Harmonic Product Spectrum (HPS)
MIT License
Copyright (c) 2021 chciken
'''
import copy
import os
import numpy as np
import scipy.fftpack
import sounddevice as sd
import time
# General settings that can be changed by the user
SAMPLE_FREQ = 48000 # sample frequency in Hz
WINDOW_SIZE = 48000 # window size of the DFT in samples
WINDOW_STEP = 12000 # step size of window
NUM_HPS = 5 # max number of harmonic product spectrums
POWER_THRESH = 1e-6 # tuning is activated if the signal power exceeds this threshold
CONCERT_PITCH = 440 # defining a1
WHITE_NOISE_THRESH = 0.2 # everything under WHITE_NOISE_THRESH*avg_energy_per_freq is cut off
WINDOW_T_LEN = WINDOW_SIZE / SAMPLE_FREQ # length of the window in seconds
SAMPLE_T_LENGTH = 1 / SAMPLE_FREQ # length between two samples in seconds
DELTA_FREQ = SAMPLE_FREQ / WINDOW_SIZE # frequency step width of the interpolated DFT
OCTAVE_BANDS = [50, 100, 200, 400, 800, 1600, 3200, 6400, 12800, 25600]
ALL_NOTES = ["A","A#","B","C","C#","D","D#","E","F","F#","G","G#"]
def find_closest_note(pitch):
"""
This function finds the closest note for a given pitch
Parameters:
pitch (float): pitch given in hertz
Returns:
closest_note (str): e.g. a, g#, ..
closest_pitch (float): pitch of the closest note in hertz
"""
i = int(np.round(np.log2(pitch/CONCERT_PITCH)*12))
closest_note = ALL_NOTES[i%12] + str(4 + (i + 9) // 12)
closest_pitch = CONCERT_PITCH*2**(i/12)
return closest_note, closest_pitch
HANN_WINDOW = np.hanning(WINDOW_SIZE)
def callback(indata, frames, time, status):
"""
Callback function of the InputStream method.
That's where the magic happens ;)
"""
# define static variables
if not hasattr(callback, "window_samples"):
callback.window_samples = [0 for _ in range(WINDOW_SIZE)]
if not hasattr(callback, "noteBuffer"):
callback.noteBuffer = ["1","2"]
if status:
print(status)
return
if any(indata):
callback.window_samples = np.concatenate((callback.window_samples, indata[:, 0])) # append new samples
callback.window_samples = callback.window_samples[len(indata[:, 0]):] # remove old samples
# skip if signal power is too low
signal_power = (np.linalg.norm(callback.window_samples, ord=2)**2) / len(callback.window_samples)
if signal_power < POWER_THRESH:
os.system('cls' if os.name=='nt' else 'clear')
print("Closest note: ...")
return
# avoid spectral leakage by multiplying the signal with a hann window
hann_samples = callback.window_samples * HANN_WINDOW
magnitude_spec = abs(scipy.fftpack.fft(hann_samples)[:len(hann_samples)//2])
# supress mains hum, set everything below 62Hz to zero
for i in range(int(62/DELTA_FREQ)):
magnitude_spec[i] = 0
# calculate average energy per frequency for the octave bands
# and suppress everything below it
for j in range(len(OCTAVE_BANDS)-1):
ind_start = int(OCTAVE_BANDS[j]/DELTA_FREQ)
ind_end = int(OCTAVE_BANDS[j+1]/DELTA_FREQ)
ind_end = ind_end if len(magnitude_spec) > ind_end else len(magnitude_spec)
avg_energy_per_freq = (np.linalg.norm(magnitude_spec[ind_start:ind_end], ord=2)**2) / (ind_end-ind_start)
avg_energy_per_freq = avg_energy_per_freq**0.5
for i in range(ind_start, ind_end):
magnitude_spec[i] = magnitude_spec[i] if magnitude_spec[i] > WHITE_NOISE_THRESH*avg_energy_per_freq else 0
# interpolate spectrum
mag_spec_ipol = np.interp(np.arange(0, len(magnitude_spec), 1/NUM_HPS), np.arange(0, len(magnitude_spec)),
magnitude_spec)
mag_spec_ipol = mag_spec_ipol / np.linalg.norm(mag_spec_ipol, ord=2) #normalize it
hps_spec = copy.deepcopy(mag_spec_ipol)
# calculate the HPS
for i in range(NUM_HPS):
tmp_hps_spec = np.multiply(hps_spec[:int(np.ceil(len(mag_spec_ipol)/(i+1)))], mag_spec_ipol[::(i+1)])
if not any(tmp_hps_spec):
break
hps_spec = tmp_hps_spec
max_ind = np.argmax(hps_spec)
max_freq = max_ind * (SAMPLE_FREQ/WINDOW_SIZE) / NUM_HPS
closest_note, closest_pitch = find_closest_note(max_freq)
max_freq = round(max_freq, 1)
closest_pitch = round(closest_pitch, 1)
callback.noteBuffer.insert(0, closest_note) # note that this is a ringbuffer
callback.noteBuffer.pop()
os.system('cls' if os.name=='nt' else 'clear')
if callback.noteBuffer.count(callback.noteBuffer[0]) == len(callback.noteBuffer):
print(f"Closest note: {closest_note} {max_freq}/{closest_pitch}")
else:
print(f"Closest note: ...")
else:
print('no input')
try:
print("Starting HPS guitar tuner...")
with sd.InputStream(channels=1, callback=callback, blocksize=WINDOW_STEP, samplerate=SAMPLE_FREQ):
while True:
time.sleep(0.5)
except Exception as exc:
print(str(exc))
The basic code has many things in common with simple DFT tuner, but of course the algorithmic parts are pretty different. Furthermore, some signal processing methods were added in order to increase the signal quality. These methods could also be applied to the DFT tuner. In the following I will provide some comments on the code:
Line 64-68: Calculate the signal power. If there is no sound, we don't need to do the signal processing part.
Line 70-71: The signal is multiplied with a Hann Window to reduce
spectral leakage.
Line 74-76: Suppress mains hum. This is a quite important signal enhacement.
Line 78-87: The average energy for a frequency band is calculated.
If the energy of a given frequency is below this average energy, then the energy is set to zero.
With this method we can reduce white noise or noise which is very close to white noise (note, that white noise has a flat spectral distribution).
This is necessary as the HPS method does not work so well if there is a lot of white noise.
Line 89-94: Here the DFT spectrum is interpolated. We need to do this as we are required to downsample the spectrum in the later steps.
Imagine there is a perfect peak at a given frequency and all the frequencies next to it are zero.
If we now downsample the spectrum, there is a certain risk that this peak is simply ignored.
This can be avoided having an interpolated spectrum as the peaks are "smeared" over a larger area.
Line 96-101: The heart of the HPS algorithm. Here the frequency scaled spectrums are multiplied
Line 103-...: Basically the same as DFT algorithm but with a majority vote filter.
Only print the note, if the previous note is the same.
Again, I also made a javascript version of this with some reduced signal enhacement as javascript is not really made for realtime signal processing.
If you compare this tuner to the previous simple tuner, you will probably notice that it already works many times more accurate. In fact, when plugging my guitar directly into the computer with an audio interface, it works perfectly. When using a simple microphone I rarely notice some harmonic errors but in general tuning the guitar is possible.
Also other people sometimes observed these harmonic erros (thank you for feedback, Valentin), so I had to investigate.
By analyzing some spectrums where the pitch was incorrectly indentified, a came across a fundamental theoretical weakness of the algorithm.
If one the overtone is missing, then the fundamental frequency is eventually multiplied by zero and consequently vanishes from the HPS.
With this current implementation this situation might also occur, if one of the harmonics was so weak that it is considered as white noise.
To counteract this phenomenon I added the
4. Summary
In this post I showed how to write a guitar tuner using Python.
We first started with a simple DFT peak detection algorithm and then refined it using a Harmonic Product Spectrum approach
which already gave us a solid guitar tuner.
In case of harsh environments or missing overtones the HPS tuner sometimes suffers from harmonic errors,
so in the future I might make more guitar tuners using different pitch detection algorithms based on cepstrums (yes, this is correct, you are not having a stroke)
or correlation.
If you like to add or critize somthing, pease contact me :)
You can do this by writing an e-mail to me (see About).